1.1 向量和线性组合

矢量和矢量之间是由区别的，就像你不能把苹果和橘子放在一起一样。看下面的二维向量：

Column vector v \(\boldsymbol{v}=\begin{bmatrix} v_{1}\\v_{2} \end{bmatrix}\)，其中\(v_{1}\)是向量\(\boldsymbol{v}\)的第一个分量，\(v_{2}\)是向量\(\boldsymbol{v}\)的第二个分量。

我们是不会将\(v_{1}\)和\(v_{2}\)相加的，但是我们可以执行向量相加：

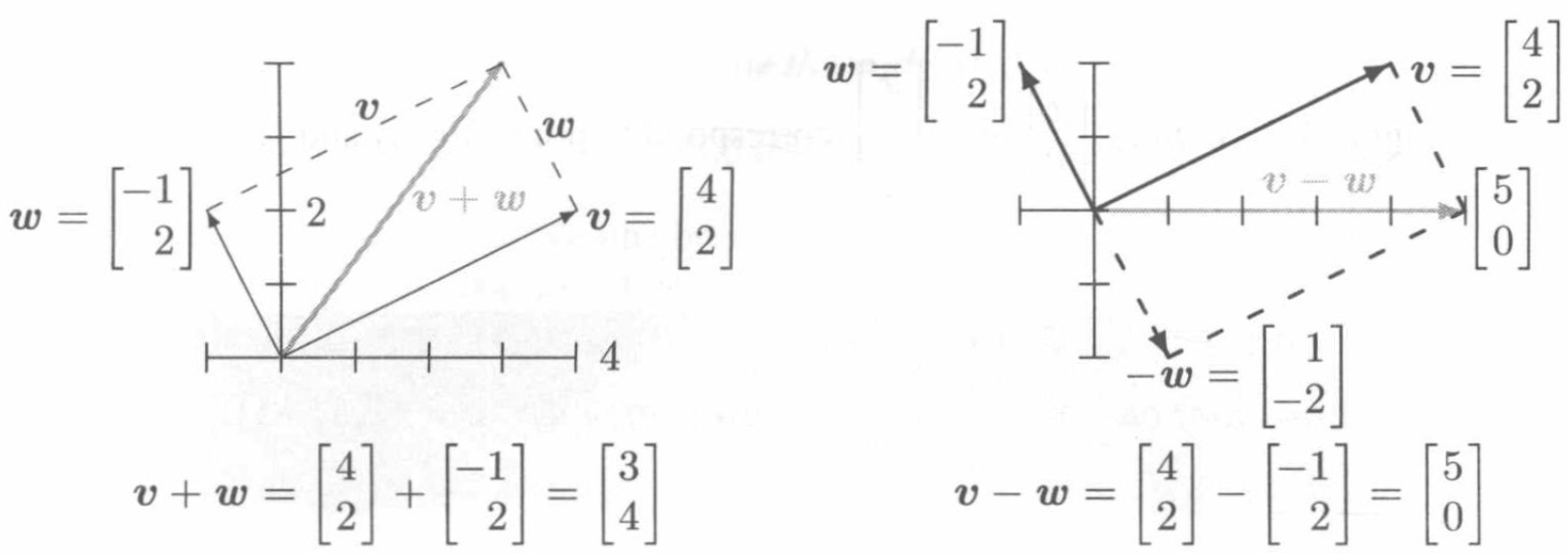
向量加法 \(\boldsymbol{v}=\begin{bmatrix}v_{1}\\v_{2} \end{bmatrix}\) 和 \(\boldsymbol{w}=\begin{bmatrix} w_{1}\\w_{2} \end{bmatrix}\)执行的是对应分量相加：\(\boldsymbol{v+w}=\begin{bmatrix} v_{1}+w_{1}\\v_{2}+w_{2} \end{bmatrix}\)。

另外，减法也是该规则，不再赘述。

还有一种运算是标量乘法。标量乘以向量，执行向量的每个分量的分别相乘：

标量乘法 \(2\boldsymbol{v}=\begin{bmatrix} 2v_{1}\\2v_{2} \end{bmatrix}=\boldsymbol{v+v} \quad -\boldsymbol{v}=\begin{bmatrix} -v_{1}\\-v_{2} \end{bmatrix}\)。

另外需要注意，\(-\boldsymbol{v}\)和\(\boldsymbol{v}\)之和是零向量，但是这个零向量不等于数字零。0是由分量0和0组成的。线性代数就是建立在这些向量运算上的。

我们将向量加法和标量乘法结合起来就得到了线性组合的方法。就像：\(c\boldsymbol{v}+d\boldsymbol{w}\)。

四种特殊的向量组合是：和、差、零以及标量相乘：

零向量总会是一个可能的组合。每次我们构建一个向量空间，就会有一个零向量被包含进去。整个向量空间，包含了所有v和w的组合。

下图展示了向量的可视化。向量可以使用箭头表示，也可以用平面上的点来表示。

1-1

那么，向量里有三个分量呢。两个分量的向量对应于xy平面上的点，而三个分量时这个xy平面被xyz三维空间所取代。另外，请注意，向量(x,y)与向量(x,y,0)是不同的。

现在开始 \(\boldsymbol{v}=\begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix}\)也可以被写为\(\boldsymbol{v}=(1,1,-1)\)

使用行的形式来写是为了节省空间，但v=(1,1,-1)绝不是行向量！要时刻记着，它是一个暂时躺着的列向量，与行向量[1,1,-1]是完全不同的。这个1行3列的行向量其实是3行1列的列向量的转置。

三维空间中，向量相加仍是各个分量加和。因此，4维、5维或n维中的向量加法都是如此。v，w，v+w在向量空间中表示出来的话，在同一个平面上。

三维空间中典型的线性组合是\(\boldsymbol{u}+4\boldsymbol{v}-2\boldsymbol{w}\)：

\(\begin{bmatrix} 1\\0\\3 \end{bmatrix} + 4\begin{bmatrix} 1\\2\\1 \end{bmatrix}-2\begin{bmatrix} 2\\3\\-1 \end{bmatrix}=\begin{bmatrix} 1\\2\\9 \end{bmatrix}\)

接下来有几个重要的问题：

对于一个向量u，线性组合cu是其唯一的线性组合可能。对于两个向量cu+dv，对于三个向量cu+dv+ew，其中cde都不做限制，uvw假设是三维空间中的向量，那么：

  1. cu的图像是如何？
  2. cu+dv图像是如何？
  3. cu+dv+ew图像是如何？

极端情况下，他们都是零向量，那么每个组合都是零。如果它们是典型的非零向量的话：

  1. cu是通过(0,0,0)填充的一条直线
  2. cu+dv是通过(0,0,0)填充的一个平面
  3. cu+dv+ew填充了整个三维空间

当然，也要去考虑一些特殊情况，上述是及其一般的情况。设想一下，如果w恰好是cu+dv的话，那也就意味着向量w就在前两个向量的平面上。uvw的组合就不会在uv平面外了。因此就得不到整个三维空间了。（你可以设想一下，xyz坐标系的建立是怎么回事，这是最标准的坐标系，即相互垂直，可以覆盖到所有三维平面上的点。但是如果z轴在xy平面上呢，这个z轴就废了，就只能是表示二维平面的点了。cu+dv等于w也就可以看作这种情况的一般化。类似的也就有了cu刚好等于v的特殊情况之类）

总之，线性组合u或uv或uvw。在三维空间上，所有的组合填充了一条线，然后是一个平面，然后是整个空间\(\mathbf{R}^3\)。

应用：

1.1 A 向量v=(1,1,0)和w=(0,1,1)的线性组合填充了一个平面\(\mathbf{R}^3\)。那么，如何找到一个不在该平面的向量呢。

首先列出v和w的所有线性组合cv+dw：

\(c\boldsymbol{v}+d\boldsymbol{w}=c\begin{bmatrix} 1\\1\\0 \end{bmatrix}+d\begin{bmatrix} 0\\1\\1 \end{bmatrix}=\begin{bmatrix} c\\c+d\\d \end{bmatrix}\)

因此，此平面的向量，第2个参数总是1、3之和。因此诸如(1,2,3)不在这个平面.

另外由于该平面穿过(0,0,0)我们知道n=(1,-1,1)垂直于这个平面。后面我们将会学到可以通过点积来确认垂直关系:\(\boldsymbol{v} \cdot \boldsymbol{n}=0\)和\(\boldsymbol{w} \cdot \boldsymbol{n}=0\)。垂直向量点积为0。

1.1 B 找到c和d的两个方程，使得线性组合cv+dw等于b：

\(\boldsymbol{v}=\begin{bmatrix} 2\\-1 \end{bmatrix}\quad \boldsymbol{w}=\begin{bmatrix} -1\\2 \end{bmatrix} \quad \boldsymbol{b}=\begin{bmatrix} 1\\0 \end{bmatrix}\)

应用数学中，解决问题通常是两个部分内容：

  1. 建模部分 用一组方程来表示问题
  2. 计算部分 用快速准确的算法解决问题

这里我们只列出方程，后续第二章在学习解法。例子可以用一个线性代数的基础模型来拟合：

找到n个数字，\(c_{1},\dots,c_{n}\)使得\(c_{1}\boldsymbol{v}_{1}+\cdots+c_{n}\boldsymbol{v}_{n}=\boldsymbol{b}\)，这里n=2：

\(cv+dw=b\qquad c\begin{bmatrix} 2\\-1 \end{bmatrix}+d\begin{bmatrix} -1\\2 \end{bmatrix} =\begin{bmatrix} 1\\0 \end{bmatrix}\)

c，d可以由以下方程得出：

两个原始方程 \(\qquad \begin{matrix} 2c-d=1\\-c+2d=0 \end{matrix}\)

每个方程产生一条直线，两条直线相交于c=2/3，d=1/3。当然我们可以用矩阵方程的形式来展现：

2×2矩阵 \(\qquad \begin{bmatrix} 2&-1\\-1&2 \end{bmatrix} \begin{bmatrix} c\\d \end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}\)