1.3 矩阵
这个部分将开始于三个向量,\(\boldsymbol{u}\),\(\boldsymbol{v}\),\(\boldsymbol{w}\)。我们将会将他们组合成矩阵:
\[\boldsymbol{u}=\begin{bmatrix} 1\\-1\\0 \end{bmatrix}\qquad\boldsymbol{v}=\begin{bmatrix} 0\\1\\-1 \end{bmatrix}\qquad\boldsymbol{w}=\begin{bmatrix} 0\\0\\1 \end{bmatrix}\]
我们有他们在三维空间的线性组合:\(x_{1}\boldsymbol{u}+x_{2}\boldsymbol{v}+x_{3}\boldsymbol{w}\):
\[\begin{equation} x_{1}\begin{bmatrix} 1\\-1\\0 \end{bmatrix}+x_{2}\begin{bmatrix} 0\\1\\-1 \end{bmatrix}+x_{3}\begin{bmatrix} 0\\0\\1 \end{bmatrix}=\begin{bmatrix}x_{1}\\x_{2}-x_{1}\\x_{3}-x_{2}\end{bmatrix} \end{equation}\]
此时,我们以矩阵的形式重写该式子,让其表示为矩阵乘以向量的形式:
\[\begin{equation} A\boldsymbol{x}=\begin{bmatrix}1&0&0\\-1&1&0\\0&-1&1\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}x_{1}\\x_{2}-x_{1}\\x_{3}-x_{2}\end{bmatrix}\end{equation}\]
矩阵A与向量x相乘的效果与前面数字与向量相乘是一样的。但是,有一些东西是不同的:首先,前面是数字去乘以向量,而后面是矩阵A作用于向量x上。输出是一个关于A的列的组合。
为了看明白A的作用,我们将Ax的结果的分量用b1-b3来表示:
\[\begin{equation}A\boldsymbol{x}=\begin{bmatrix}1&0&0\\-1&1&0\\0&-1&1\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}x_{1}\\x_{2}-x_{1}\\x_{3}-x_{2}\end{bmatrix}=\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}=\boldsymbol{b}\end{equation}\]
A被称为差矩阵,因为b包含了向量x的差。也就是说如果向量x=(1,4,9)那么向量b就是(1,3,5)了,实为x向量中前后两项之差。如果是4×4矩阵亦然。
重点:每一次都是对一整行进行乘法运算。矩阵与向量的成分通常是使用矩阵每行对于向量的点积:
Ax也是行的点积\[\begin{equation}\qquad A\boldsymbol{x}=\begin{bmatrix}1&0&0\\-1&1&0\\0&-1&1\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}(1,0,0)\cdot(x_{1},x_{2},x_{3})\\(-1,1,0)\cdot(x_{1},x_{2},x_{3})\\(0,-1,1)\cdot(x_{1},x_{2},x_{3})\end{bmatrix}\end{equation}\]
点积形式的结果与公式(3)相同。新的方法是将Ax按列进行处理。对于数字来说你可以将Ax按行相乘;对于字母来说,按列来处理是一个好方法。第2章我们会回来详细解释。
线性方程
前面我们有\(A\boldsymbol{x}=\boldsymbol{b}\),那么现在如果知道b要怎么求x呢?于是,就有了如下方程:
\[\begin{equation} 方程A\boldsymbol{x}=\boldsymbol{b}\quad \begin{matrix}x{1}=b{1}\\-x{1}+x{2}=b{2}\\-x{2}+x{3}=b{3}\end{matrix}\qquad 解\boldsymbol{x}=A^{-1}\boldsymbol{b}\quad \begin{matrix}x{1}=b{1}\\x{2}=b{1}+b{2}\\x{3}=b{1}+b{2}+b{3}\end{matrix} \end{equation}\]
这个方程可以按顺序从上到下依次解开,因为A是一个三角矩阵。此时的矩阵A是可逆的。
逆矩阵
让我们再来看(5)中方程的解。我们可以从中发现一个和矩阵:
\[\begin{equation} \begin{bmatrix}x{1}\\x{2}\\x{3}\end{bmatrix}=\begin{bmatrix}b{1}\\b{1}+b{2}\\b{1}+b{2}+b{3}\end{bmatrix}=\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\end{bmatrix}\begin{bmatrix}b{1}\\b{2}\\b{3}\end{bmatrix} \end{equation}\]
x是b的差,b是x的和。公式(6)中的和矩阵是差矩阵\(A\)的逆矩阵\(A^{-1}\)。
公式(6)告诉了我们两个重要的事实:
- 对于每个\(\boldsymbol{b}\)都有\(A\boldsymbol{x}=\boldsymbol{b}\)。
- 矩阵\(A^{-1}\)给出了解\(x=A^{-1}\boldsymbol{b}\)。
下一章将会虚招更多的Ax=b的方程,看看他们的解。
接下来,让我们将矩阵求解与微积分进行一个对比。我们把向量\(\boldsymbol{x}\)变成函数\(x(t)\)。差\(A\boldsymbol{x}\)变成导数\(dx/dt=b(t)\)。那么逆过程\(A^{-1}\boldsymbol{b}\)就变成了\(b(t)\)的积分。差的和就相当于是对导数的积分。
根据微积分的基础:积分就是微分的逆运算。
\[\begin{equation} A\boldsymbol{x}=\boldsymbol{b} \quad \boldsymbol{and}\quad \boldsymbol{x}=A^{-1}\boldsymbol{b}\qquad \frac{dx}{dt}=b \quad and \quad x(t)=\int_{0}^{t}b\ dt \end{equation}\]
比如我们的\(x(t)=t^2\),其导数就是2t。当t为1,2,3时,b是2,4,6。但是我们通过差矩阵得到的结果是2t-1而不是2t。
循环差分
下面,我们来使用一个新的向量\(\boldsymbol{w}^{*}\)
\[\boldsymbol{u}=\begin{bmatrix} 1\\-1\\0 \end{bmatrix}\qquad\boldsymbol{v}=\begin{bmatrix} 0\\1\\-1 \end{bmatrix}\qquad\boldsymbol{w}^{*}=\begin{bmatrix} -1\\0\\1 \end{bmatrix}\]
此时再将它们线性组合起来就得到了一个循环差分矩阵C:
\[\begin{equation} C\boldsymbol{x}=\begin{bmatrix}1&0&-1\\-1&1&0\\0&-1&1\end{bmatrix}\begin{bmatrix}x{1}\\x{2}\\x{3}\end{bmatrix}=\begin{bmatrix}x{1}-x{3}\\x{2}-x{1}\\x{3}-x{2}\end{bmatrix}=\boldsymbol{b} \end{equation}\]
这个矩阵C不是三角矩阵。实际上这个\(C\boldsymbol{x}=\boldsymbol{b}\)的方程是无解的,因为它可以找到无穷多解或0个解:
\[\begin{equation} C\boldsymbol{x}=\boldsymbol{0}:\begin{bmatrix}x{1}-x{3}\\x{2}-x{1}\\x{3}-x{2}\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix}:\begin{bmatrix}x{1}\\x{2}\\x{3}\end{bmatrix}=\begin{bmatrix}c\\c\\c\end{bmatrix} \end{equation}\]
那么,如果取\(\boldsymbol{b}=(1,3,5)\):
\[\begin{equation} \begin{bmatrix}x{1}-x{3}\\x{2}-x{1}\\x{3}-x{2}\end{bmatrix}=\begin{bmatrix}1\\3\\5\end{bmatrix} \end{equation}\]
等式左右相加不相等,明显无解。让我们从几何的角度来看待这个问题。由(1),b就可以看作是向量\(u,v,w^{*}\)的线性组合。没有任何线性组合可以产生向量\(\boldsymbol{b}=(1,3,5)\)。右侧需要满足\(b{1}+b{2}+b{3}=0\)。
在几何上,所有的线性组合\(x_{1}\boldsymbol{u}+x_{2}\boldsymbol{v}+x_{3}\boldsymbol{w}^{*}\)都在一个平面\(b{1}+b{2}+b{3}=0\)上。
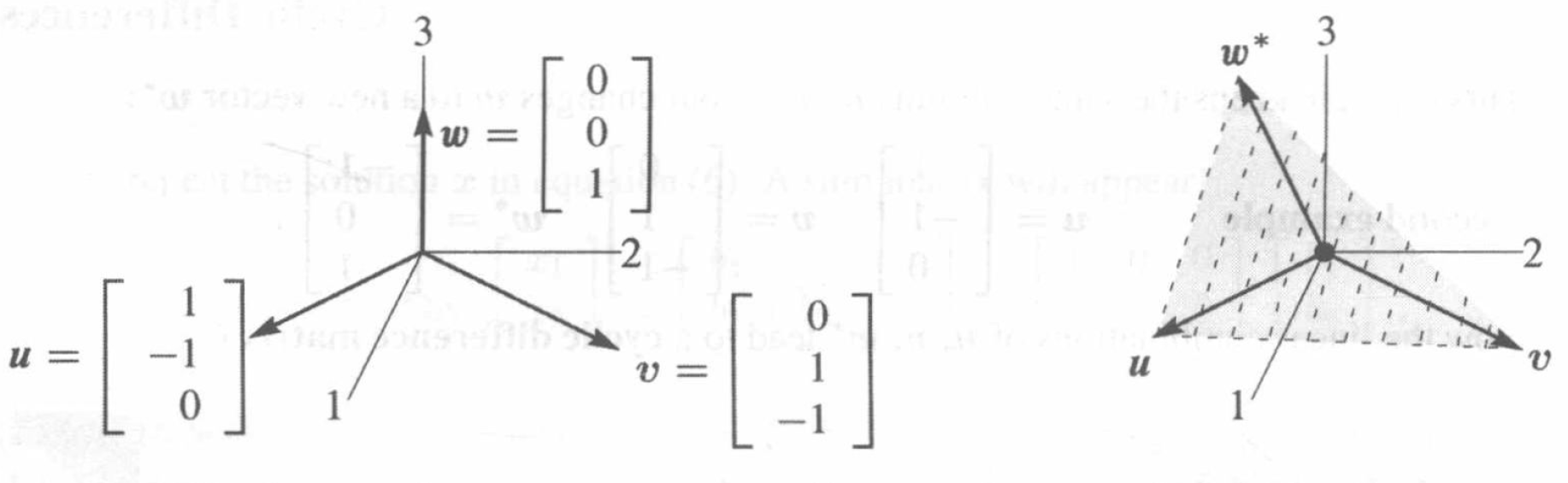
独立和相关
上图展示了这些列向量,无论是矩阵A还是C,前两个列向量是相同的,就是第三个不同。如果我们只根据前两个向量是可以得到一个二维平面的。问题的关键就在于这第三个向量在不在这个平面上。
- 独立:\(\boldsymbol{w}\)不在\(\boldsymbol{u}\boldsymbol{v}\)的平面上
- 相关:\(\boldsymbol{w^{*}}\)在\(\boldsymbol{u}\boldsymbol{v}\)的平面上
那么前面判断向量是否在同一平面的方法就可以拉过来了。我们可以知道\(\boldsymbol{u}\boldsymbol{v}\)平面可以表示为线性组合\(c\boldsymbol{v}+d\boldsymbol{w}\),只要能找到\(\boldsymbol{w}=c\boldsymbol{v}+d\boldsymbol{w}\)就说明他们在一个平面上。
因此:
- 独立列向量:\(A\boldsymbol{x}=\boldsymbol{0}\)有一个解。A被称为可逆矩阵。
- 相关列向量:\(C\boldsymbol{x}=\boldsymbol{0}\)有许多解。A被称为奇异矩阵。