2.4 矩阵运算规则
- 矩阵A有n列乘以矩阵B有n行:\(A_{m\times n}B_{n\times p}=C_{m\times p}\)。
- \(AB=C\)的每个分项都是一个点乘:\(C_{ij}=(A的i行)\cdot (B的j列)\)。
- AB乘以C等于A乘以BC。
- 有更多的方法来计算AB:(A乘B的列)(A的行乘B)(列乘行)。
- 往往不会有AB=BA。大多数情况下,AB不能互通。
- 矩阵可以按块相乘:\(A=[A_1\quad A_2]\)乘以\(B=\begin{bmatrix}B_1\\B_2\end{bmatrix}\)同\(A_1B_1+A_2B_2\)。
矩阵乘法不像矩阵加法,矩阵加法只要维度相同就能相加,而矩阵乘法是否可以执行,需要看是否满足:如果要实现矩阵乘法AB,则需要A有n列,B必须有n行。
而且我们知道A(BC)=(AB)C的。另外如果A是m×n,B是n×p的话,那么AB就是m×p。这些都是线性代数的规则。
首先我们来看乘法运算的第一个方法,也是常用的方法。将A的每行与B的每列取点积:
|
就像下图2-8所示:
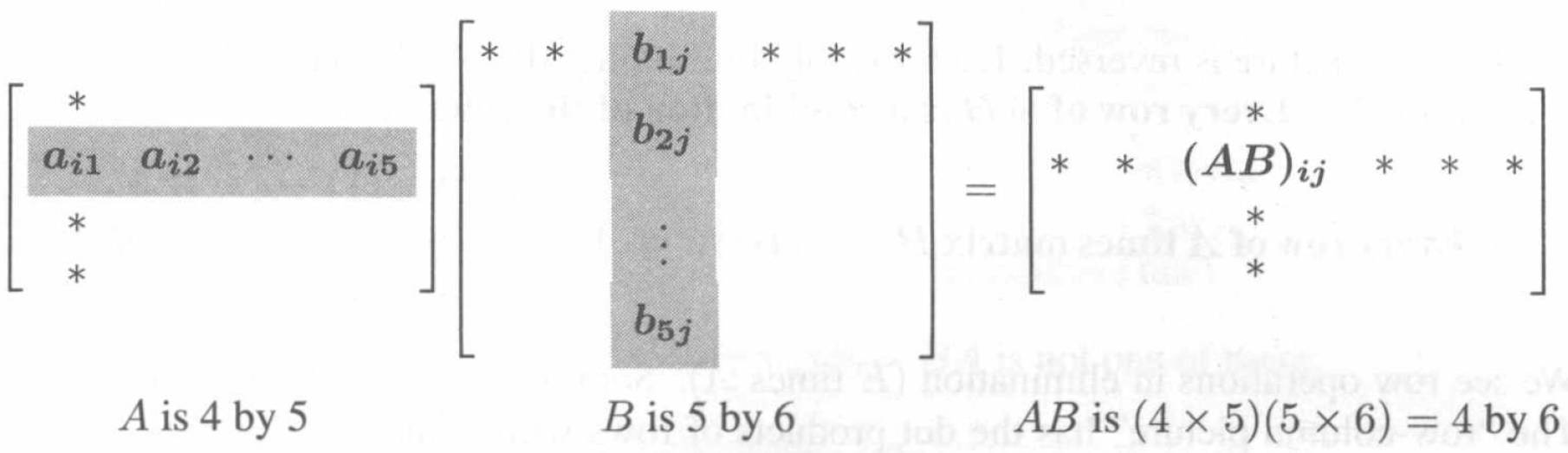
如果AB都是方阵n×n的话,会有\(n^2\)个点积,每个点积也都是由n个乘法相加的,所以AB用了\(n^3\)个单独的乘法运算。后来呢也有人通过将n×n分解成2×2的块的方法来减少大矩阵的计算。计算数量下降到了\(n^{2.376}\)。但是科学计算还是需要常规的\(n^3\)次运算的。
一行乘一列以及一列乘一行的操作都是合理的。前者叫做内积,这也是点积的另一个名称。后者叫做外积,这些都是极端情况的矩阵乘法。
第二种和第三章方法:行和列
A乘以B的一列,其结果是AB的一列。这一列中,我们将A的每一列进行组合,这就是矩阵乘法的列算法:
|
行算法刚好反过来,A的每行都乘以整个矩阵B。结果就是AB的每行:
|
第四种方法:列乘以行
- 将A的第1到n列乘以B的第1到n行。然后将这些矩阵相加:
\[\begin{bmatrix}col1&col2&col3\\.&.&.\\.&.&.\end{bmatrix}\begin{bmatrix}row1&.&.&.\\row2&.&.&.\\row3&.&.&.\end{bmatrix}=(col1)(row1)+(col2)(row2)+(col3)(row3)\]
比如2×2的矩阵,注意看:
\[AB=\begin{bmatrix}\boldsymbol{a}&b\\ \boldsymbol{c}&d\end{bmatrix}\begin{bmatrix}\boldsymbol{E}&\boldsymbol{F}\\G&H\end{bmatrix}=\begin{bmatrix}\boldsymbol{aE}+bG&\boldsymbol{aF}+bH\\\boldsymbol{cE}+dG&\boldsymbol{cF}+dH\end{bmatrix}\]
\[\begin{equation} 行列相乘再相加:\boldsymbol{AB}=\begin{bmatrix}\boldsymbol{a}\\\boldsymbol{c}\end{bmatrix}\begin{bmatrix}\boldsymbol{E}&\boldsymbol{F}\end{bmatrix}+\begin{bmatrix}b\\d\end{bmatrix}\begin{bmatrix}G&H\end{bmatrix} \end{equation}\]
矩阵运算定律
矩阵满足的六条定律,其中涉及加法的定律都很简单,下面是三条:
\(A+B=B+A(交换律)\) \(c(A+B)=cA+cB(分配律)\) \(A+(B+C)=(A+B)+C(结合律)\)
三条乘法定律:
\(AB=BA(交换律通常不存在)\) \(A(B+C)=AB+AC(左侧分配律)\) \((A+B)C=AC+BC(右侧分配律)\) \(A(BC)=(AB)C(ABC结合律)\)
但是,AI=IA是存在的。所有的方阵都可以与I或者cI交换。
还有以下定律也是存在的:
\(A^p=AAA\cdots A(p个)\qquad(A^p)(A^q)=A^{p+q}\qquad (A^p)^q=A^{pq}\)
当pq是0或负值的时候,该公式依然存在。前提是A的逆矩阵\(A^{-1}\)存在,然后\(A^0=I\)。
块矩阵和块乘法
矩阵可以被分割成块。下面是一个4×6的矩阵被分割成2×2的块的例子,这里每块都是一个单位矩阵I:
\[A=\left[\begin{array}{cc|cc|cc} 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1\\ \hline 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1\\ \end{array}\right]=\begin{bmatrix}I&I&I\\I&I&I \end{bmatrix}\]
如果B也是4×6矩阵也可以如此分块,就可以执行A+B的块相加。
之前其实已经使用过块矩阵的概念了。当时的增广矩阵就是将向量b加到矩阵A的右侧。然后[A b]可以被消除矩阵相乘得到[EA Eb]。
块乘法:如果A的块可以乘以B的块,那么AB的块乘法就是允许的。切块后A的列必须要匹配B的行。
\[\begin{equation} \begin{bmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix}\begin{bmatrix}B_{11}\\B_{21}\end{bmatrix}=\begin{bmatrix}A_{11}B_{11}+A_{12}B_{21}\\A_{21}B_{11}+A_{22}B_{21}\end{bmatrix} \end{equation}\]
有一个特殊的块乘法的例子,可以用于推导出矩阵运算的方法四,列乘行:
矩阵AB被分为n列和n行:
\[\begin{equation}[a_1\cdots a_n]\begin{bmatrix}b_1\\.\\.\\.\\b_n\end{bmatrix}=[a_1b_1+\cdots +a_nb_n]\end{equation}\]
下面我们来看如何对块执行消去呢?假设我们有一个四个块组成的矩阵,来看看E如何消去C块的:
\[\left[ \begin{array}{c|c} I&0\\ \hline -CA^{-1}&I \end{array}\right] \left[ \begin{array}{c|c} A&B\\ \hline C&D \end{array}\right] \left[\begin{array}{c|c} A&B\\ \hline 0&D-CA^{-1}B \end{array}\right] \]
这是普通的消去,一次一列。主元是A,最后的一个块是\(D-CA^{-1}B\),他就像d-cb/a一样。这被称作是舒尔体(Schur complement)。