2.1 向量和线性方程

关于\(A\boldsymbol{x}=\boldsymbol{b}\)的列模式（column picture）：一个关于A的n列的线性组合产生了向量b。
向量方程\(A\boldsymbol{x}=x_{1}\boldsymbol{a}_{1}+\cdots+x_{n}\boldsymbol{a}_{n}=\boldsymbol{b}\)：其中\(a_{1},a_{2},\dots,a_{n}\)是由A的列组成。
当\(\boldsymbol{b}=\boldsymbol{0}\)的时候，\(A\boldsymbol{x}\)也为0，一种可能的情况是\(\boldsymbol{x}=(0,\dots,0)\)。
关于\(A\boldsymbol{x}=\boldsymbol{b}\)的行模式（row picture）：来自m行的m个方程确定了m个平面的交点为\(\boldsymbol{x}\)。
点积给出了方程中的每个平面：\((\mathbf{row\ 1}) \cdot \boldsymbol{x}=b_{1},\dots ,(\mathbf{row\ 2}) \cdot \boldsymbol{x}=b_{m}\)。
当\(\boldsymbol{b}=\boldsymbol{0}\)的时候，所有平面\((\mathbf{row\ i}) \cdot \boldsymbol{x}=0\)相交于\(\boldsymbol{x}=(0,0,\dots,0)\)。

线性代数的中心问题是求解方程组。这些方程组都是现行的，也就是未知数只能和数字相乘，而不能出现诸如x乘以y。首先，我们来看2个方程两个未知数的情况：

\[\begin{align} x-2y&=1\notag \\ 3x+2y&=11 \end{align}\]

我们从第一行开始，这一行\(x-2y=1\)产生了一条xy平面上的直线，线上的点都是方程的解。这条直线的斜率是\(\frac{1}{2}\)，因为y增长1的时候x会增长2。斜率在微积分和线性代数中同样的重要！

下图2.1就展示了方程所代表的两条直线的交点，解开了这个方程。

图2-1 行图：点(3,1)是两条直线的交点

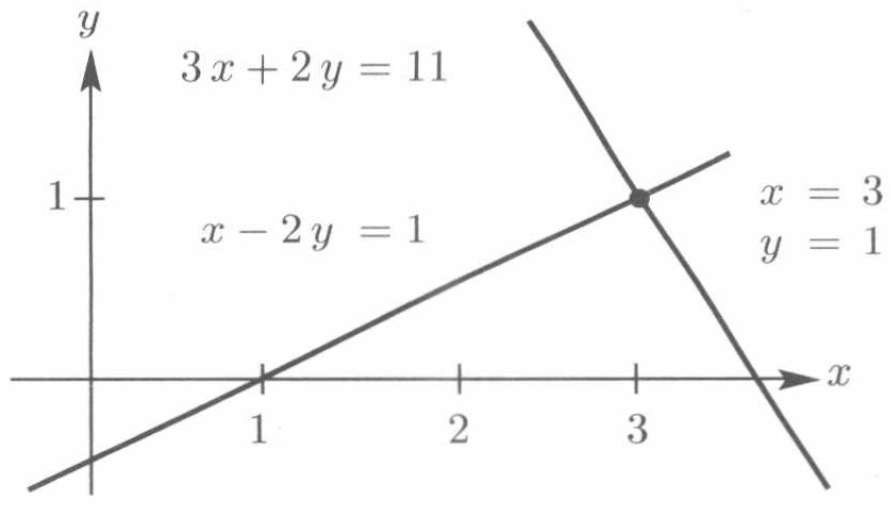
行：行图展示了两条交于单个点的方程的解。

现在，切换列模式看看。我想要称这样的线性方程为“向量方程”。我们看到的不是数字而是向量了。如果你把原方程按列分开，就会得到一个向量方程：

\[\begin{equation} x\begin{bmatrix}1\\3\end{bmatrix}+y\begin{bmatrix}-2\\2\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix}=\boldsymbol{b} \end{equation}\]

左侧是两个列向量。问题在于如何找到这些向量的线性组合来构建等式右侧。后来我们找到了x=3，y=1（自然与前面结果是一样的），来产生\(3(\boldsymbol{column\ 1})+1(\boldsymbol{column\ 2})=\boldsymbol{b}\)。

列：列图中将左侧的列向量进行组合来产生右侧的向量。

如下图2-2所示，我们得到了相应的2方程2未知数的列图。

图2-2 列图：列向量的组合产生了右侧的(1,11)

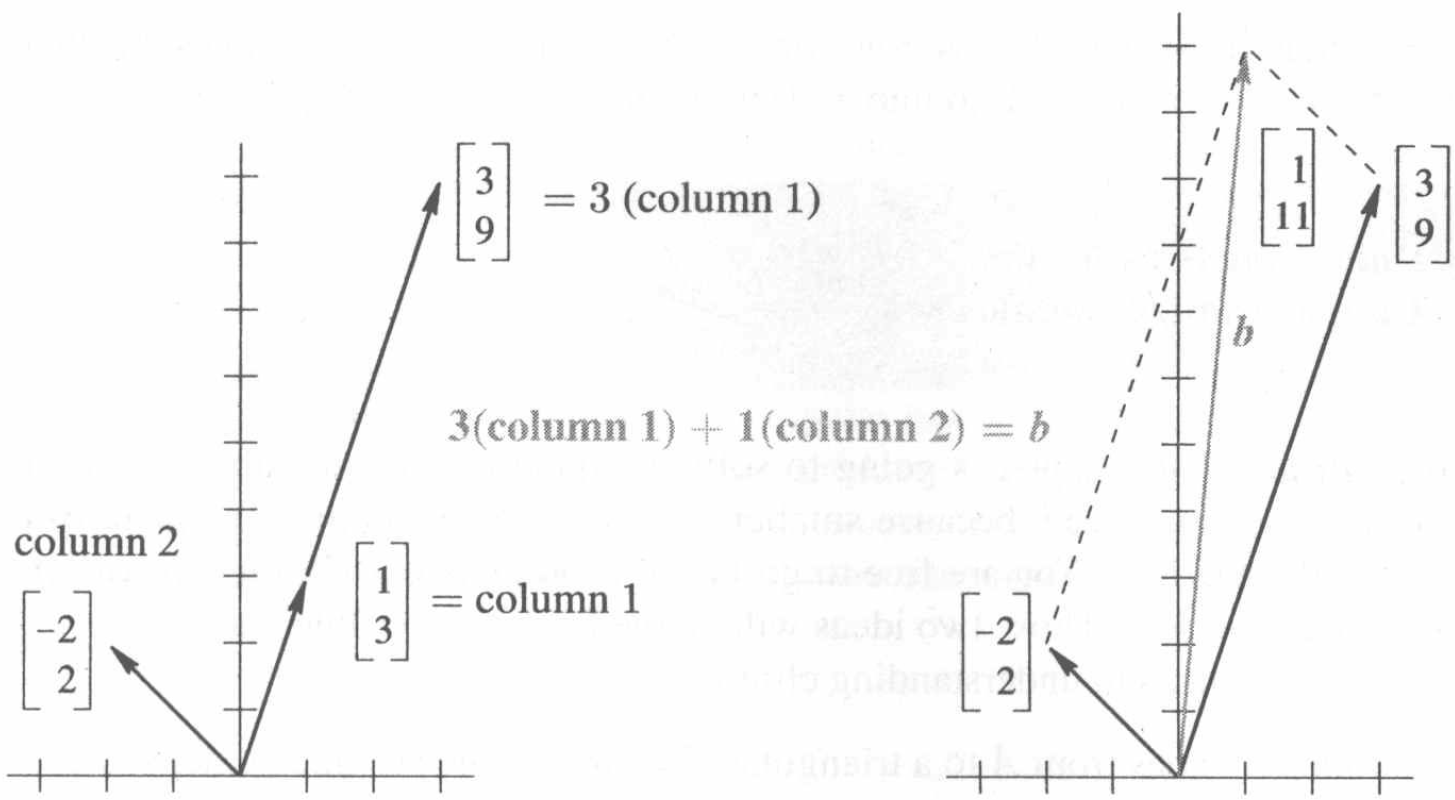
总体看来：左侧是向量方程按照列进行的线性组合。问题是如何找到x=3和y=1。我们结合了乘以标量和向量加法来实现这一组合。这一步非常重要，因为他用到了两个基本运算：

线性组合\(\qquad 3\begin{bmatrix}1\\3\end{bmatrix}+\begin{bmatrix}-2\\2\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix}\)

无论使用行的方法还是列，它们的结果当然是一致的。我不知道你会更喜欢哪种方式。假设你对于两行的式子更加熟悉，那么你可能会更喜欢使用行的方法，但是很快会改变的。我是更喜欢列向量的线性组合。因为你想要去看到一个四维空间的四个向量的组合是比你去看到四个超平面相交于一个点要更容易的（即使是一个超平面都很难去想象）

左侧方程产生了一个2×2的系数矩阵A：

\[A=\begin{bmatrix}1&-2\\3&2\end{bmatrix}\]

去从行和列的角度来看一个矩阵是在线性代数中是非常典型的方法。行给出了我们行图，列给出了列图。同样的数字，同样的方程，不一样的图示。我们用矩阵方程的形式来展示前面的方程：

矩阵方程\(A\boldsymbol{x}=\boldsymbol{b}\qquad\begin{bmatrix}1&-2\\3&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix}\)

因此，通过行和列的形式，我们有了矩阵向量相乘的方法：行的点乘法或者列的组合法。

本章是要解决n个方程n个未知数的。要对矩阵的乘法和逆运算很清楚，这两个是可逆矩阵的关键。

矩阵的消去法有四个步骤：

通过一系列矩阵步骤Eij将矩阵A消去至一个三角矩阵U。
三角矩阵通过从下到上的反向代换求解。
矩阵语言中A被分解成了LU=(下三角)(上三角)。
如果矩阵A可逆则消去成功（可能需要行交换）。

三个方程和三个未知数

来到三个未知数，有如下方程：

\[\begin{align} x+2y+3z&=6\notag \\ A\boldsymbol{x}=\boldsymbol{b} \qquad\qquad 2x+5y+2z&=4\\ 6x-3y+z&=2 \notag \end{align}\]

我们寻找xyz来解这个方程，当然解可能存在也可能不存在，对于这个方程组来说，解是存在的。当未知数和方程数相等时，解往往是一个。

解这个方程前，我们来看这两种方法：

行 行图展示了三个平面交于一个点。

列 列图将三个列向量进行组合得到 \(\boldsymbol{b}=(6,4,2)\)。

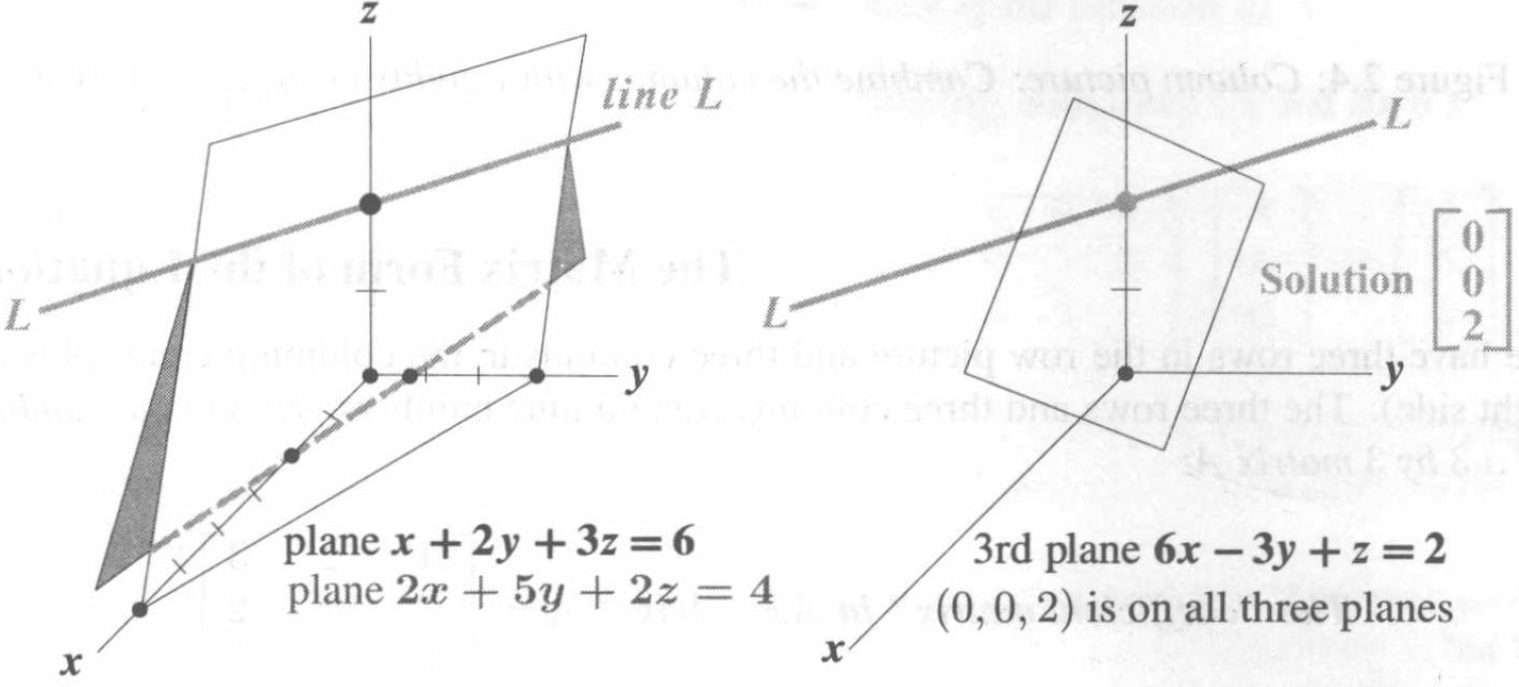
关于行的图示（图2-3），我们可以看到首先前两个方程确定了一条共直线，往往两个方程三个未知数的解就是一条直线。第三个方程给出了第三个平面。它将直线L在一点切断。这个点就是在所有三个平面上的。这是行的形式，往往去想象一个三平面交于一点是比较困难的。列形式将会立刻向你展示为什么z=2。

图2-3 行图示：两平面交于直线L。三平面交于一点。

列图开始于方程\(A\boldsymbol{x}=\boldsymbol{b}\)中的向量：

\[\begin{equation} x\begin{bmatrix}1\\2\\6\end{bmatrix}+y\begin{bmatrix}2\\5\\-3\end{bmatrix}+z\begin{bmatrix}3\\2\\1\end{bmatrix}=\begin{bmatrix}6\\4\\2\end{bmatrix}=\boldsymbol{b} \end{equation}\]

未知数是系数x，y，z。三个向量的乘法产生了向量b。

列图由图2-4展示，线性组合产生了向量b。结果显而易见。

图2-4 列图示：列通过权重(x,y,z)=(0,0,2)进行组合

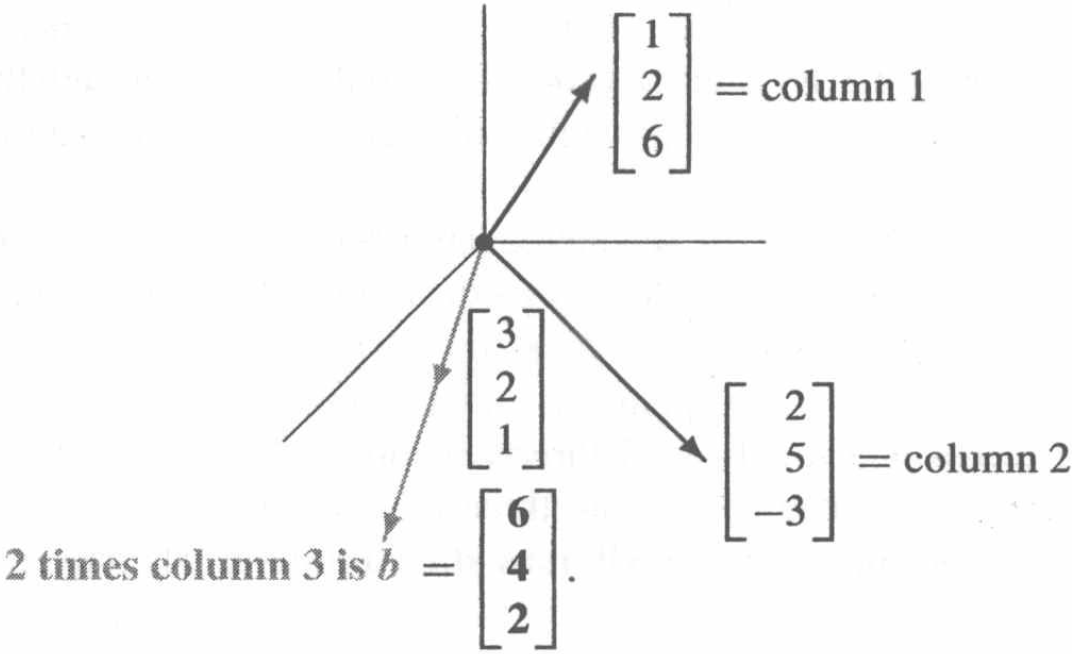
从方程而来的矩阵

将方程中未知数的系数提取出来，就形成了系数矩阵A（以（3）为例）：

\[A=\begin{bmatrix}1&2&3\\2&5&2\\6&-3&1\end{bmatrix}\]

按行计算，方程是（3）；按列计算，方程是（4）；按矩阵方程就是（5）：

\[\begin{equation} 矩阵方程\ A\boldsymbol{x}=\boldsymbol{b}\qquad\begin{bmatrix}1&2&3\\2&5&2\\6&-3&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}6\\4\\2\end{bmatrix} \end{equation}\]

A乘x怎么计算呢？我们可以按行或按列计算。

按行相乘 \(A\boldsymbol{x}\)就是点乘，每行去乘以列\(\boldsymbol{x}\)： \[\begin{equation} A\boldsymbol{x}=\begin{bmatrix}(\boldsymbol{row\ 1})\cdot \boldsymbol{x}\\(\boldsymbol{row\ 2})\cdot \boldsymbol{x}\\(\boldsymbol{row\ 3})\cdot \boldsymbol{x}\end{bmatrix} \end{equation}\]

按列相乘 \(A\boldsymbol{x}\)就是一个列向量的组合： \[\begin{equation} A\boldsymbol{x}=x(\boldsymbol{column\ 1})+y(\boldsymbol{column\ 2})+z(\boldsymbol{column\ 3}) \end{equation}\]

下面举个例子，有两个矩阵A和I（单位矩阵）：

\[A\boldsymbol{x}=\begin{bmatrix}1&0&0\\1&0&0\\1&0&0\end{bmatrix}\begin{bmatrix}4\\5\\6\end{bmatrix}=\begin{bmatrix}4\\4\\4\end{bmatrix}\qquad I\boldsymbol{x}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}4\\5\\6\end{bmatrix}=\begin{bmatrix}4\\5\\6\end{bmatrix}\]

可以试着从行和列的角度来进行运算。这个I矩阵是个特殊的存在，他只有一个主对角线上有数字1，其余都是0。我们把它叫做单位矩阵，就像乘以1一样：\(I\boldsymbol{x}=\boldsymbol{x}\)。

矩阵表示法

2×2矩阵的第一行包含了\(a_{11}\)和\(a_{12}\)。第二行就是\(a_{21}\)和\(a_{22}\)了，但是吧这些下标打起来很费劲，所以我们使用A(i,j)来替代\(a_{ij}\)：

\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}=\begin{bmatrix}A(1,1)&A(1,2)\\A(2,1)&A(2,2)\end{bmatrix}\]

MATLAB中的乘法

首先我们来看MATLAB中怎么去定义A和x的。这是学习语言的第一步。一个在\(R^n\)中的向量x可以看作是n×1的矩阵。矩阵一次输入一行，然后用分号分隔，或者直接按列输入然后使用'进行转置：

A=[1 2 3; 2 5 2; 6 -3 1] x=[0 0 2]’ 或 x=[0; 0; 2]

有三种方法来表示\(A\boldsymbol{x}\):

矩阵乘法：b=A*x
按行乘：b=[A(1,:)x; A(2,:)x; A(3,:)*x]
按列乘：b=A(;,1)x(1)+A(:，2)x(2)+A(:,3)*x(3)

矩阵可能是按照列存储的，所以按列计算会快一些，且A*x也是按列计算的。

其他语言

有五种重要的语言都有相应的命令来实现\(A\boldsymbol{x}\)：

Julia: Ax Python: dot(A,x) R: A%%x Mathematica: A.x Maple: A*x

Julia，Python，R都是开源软件。Julia结构简单，速度块；Python流行率广；R专门为统计而生。

Mathematica和Maple允许出现字母，而不仅仅是单纯的数字，作为MATLAB的符号工具，它们开源处理类似\(x^2-x\)这样的符号运算。