2.2 消元法
- 对于m=n=3,有三个方程\(A\boldsymbol{x}=\boldsymbol{b}\)和三个未知数。
- 前两个方程是\(a_{11}x_1+\cdots=b_1\)和\(a_{21}x_1+\cdots=b_2\)。
- 将第一个方程乘以\(a_{21}/a_{11}\)然后减去第二个方程:\(x_1\)就完成了消元。
- 角落的\(a_{11}\)项是第一个主元,\(a_{21}/a_{11}\)是第一个乘数。
- 消去\(x_1\)需要从剩下的所有方程i中减去\(a_{i1}/a_{11}\)乘以第一个方程。
- 现在上一个n-1个方程包含了n-1个未知数。同样的方法去消去\(x_2\)。
- 主元中如果出现了0那么就会无法消元。交换两个方程可能会解决这个事情。
这章解释了求解线性方程的具体方法,也就是消元法。看下面的2×2矩阵,消元前x和y是在两个方程中的,消元后,第一个未知数x在第二个方程中消失了:
\[\begin{align} 消元前:\quad \begin{matrix}x-2y=1\\3x+2y=11\end{matrix}\qquad消元后:\quad \begin{matrix}x-2y=1\\8y=8\end{matrix} \notag \end{align}\]
新方程可以得到y=1,回代后得到x=3,因此方程可解。
消元构造了一个上三角系统,这是它的目标。从三角系统的最下面得到的结果向上逐层带入来求解的过程叫做回代。这通常被用作上三角系统。
下面来看:原始方程也有同样的解。下图2-5展示了消元前后两个系统,方程被展示为两条线,其相交于方程的解对应的点。
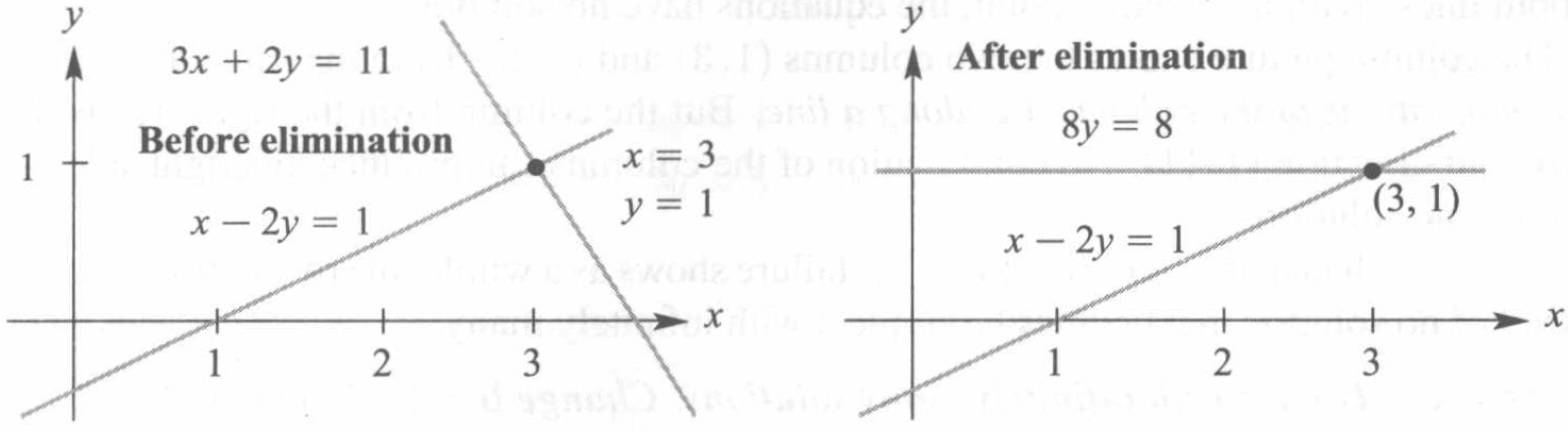
我们如何从消元前的线找到消元后的线呢?是通过将第二个方程减去第一个方程乘以3后得到的。差不多是这样的:
消去x的方法:将第2个方程减去第1个方程的倍数
上述情况是将第一个方程乘以一个乘数\(l=3\),这个乘数如何得到?第一个方程包含1x,所以第一个主元就是1(x的系数)。第二个方程包含3x,所以乘数就是3。相减后就得到了0和三角形。
乘数的规则似乎跃然纸上。如果是下面的例子,这个乘数就是\(l=\frac{3}{4}\):
\[\begin{matrix}4x-8y=4\\3x+2y=11\end{matrix}\qquad \begin{matrix}消元后\\(方程2减去方程1乘\frac{3}{4})\end{matrix} \begin{matrix}4x-8y=4\\8y=8\end{matrix}\]
因此:
|
主元(pivot) = 要被消去的行内第一个非零数 乘数(multiplier)=被消元项除以主元=3/4 |
消元后的主元在三角形的对角线上。
消元法可能存在的问题
通常情况下,消元法产生的主元会帮我们解开方程。但是也有可能会失败的。一些情况,可能会让我们去除以0,这是做不到的。可能会有一些方法来调整后继续,或者会无法消元。
下面两个例子代表性的说明了两种失败的情况。例1因为无解而失败;例2因为有太多解而失败;例3在交换方程后成功了。
例1:
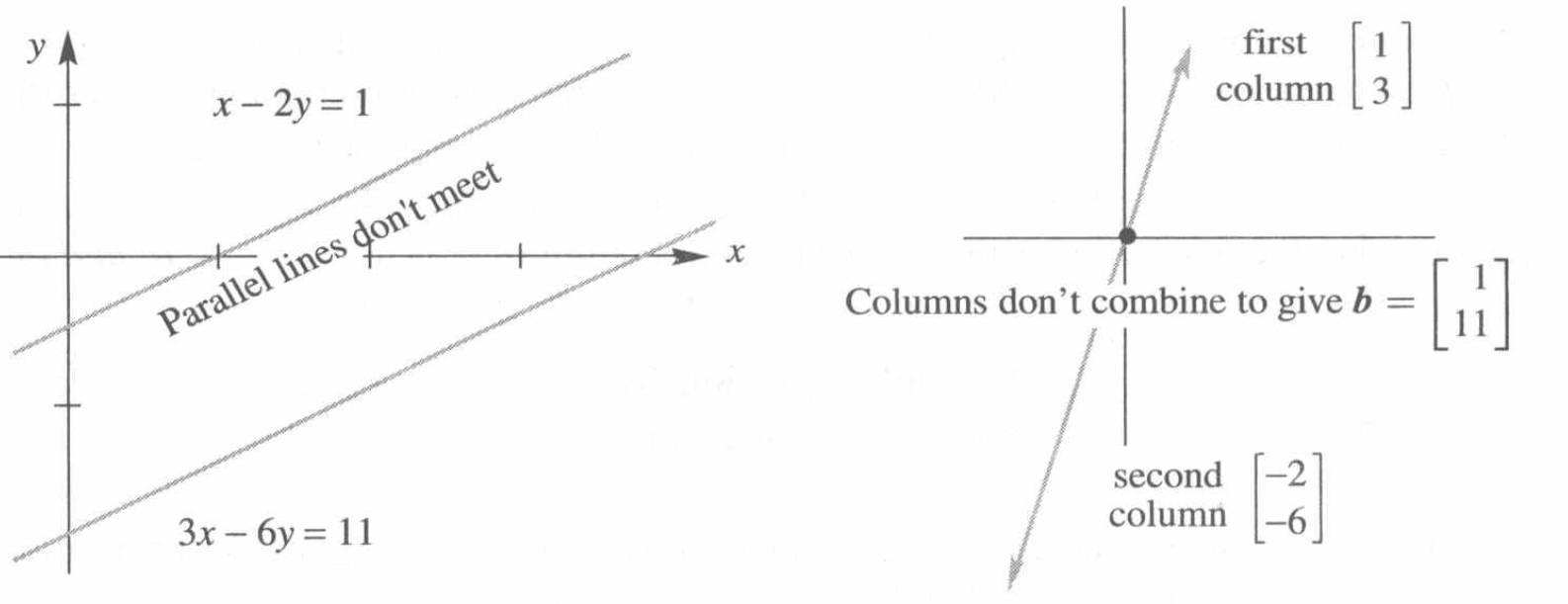
\[\begin{matrix}x-2y=1\\3x-6y=11\end{matrix}\qquad \begin{matrix}消元后\\(方程2减去方程1乘3)\end{matrix} \begin{matrix}x-2y=1\\0y=8\end{matrix}\]
明显无解。看行图列图也能看出,两条线无交点,两条向量处于同一直线。那么如果我们将方程右边改为1,3,整条直线都是解,也就是例2。
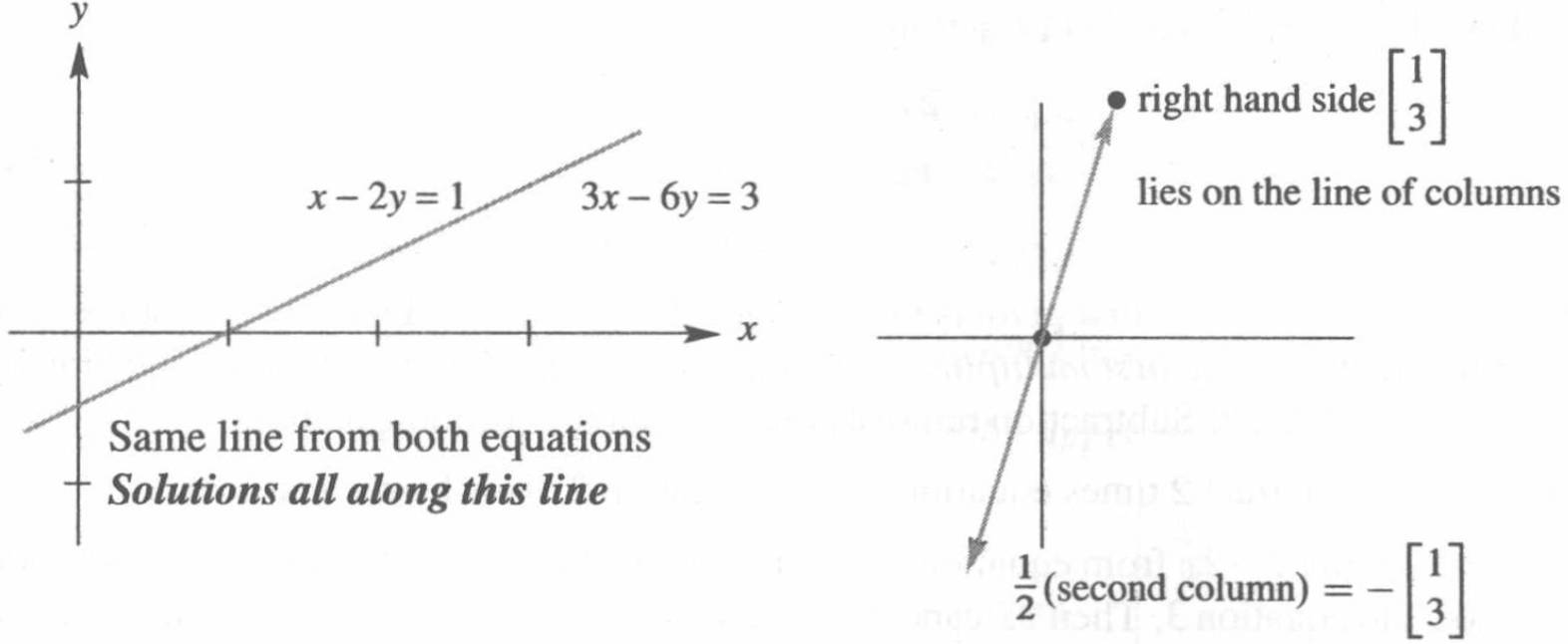
例2: \[\begin{matrix}x-2y=1\\3x-6y=3\end{matrix}\qquad \begin{matrix}消元后\\(方程2减去方程1乘3)\end{matrix} \begin{matrix}x-2y=1\\0y=0\end{matrix}\]
这里所有的y都可以满足0y=0。它的行图列图如下,可以看到方程有无数解。
例3:
主元为0,但是可以通过交换来解决:
\[\begin{matrix}0x+2y=4\\3x-2y=5\end{matrix}\qquad 交换两个方程 \begin{matrix}3x-2y=5\\2y=4\end{matrix}\]
交换后,方程本身就是三角形的了。已经可以回代进行求解了。
例子1和2是奇异的——它们没有第二个主元了。例子3是非奇异的——它们有完整的主元且只有一个解。奇异的方程没有解或有无穷多解,主元必须不为0,因为我们要除以它们。
三个方程三个未知数
其实方法是类似的,或许你没有学习过本章节也早已经会解这些方程了,但是请耐心,经过这样的过程,将会对于消元有更加深刻的理解。让我们继续:
如下方程:
\[\begin{align} 2x+4y-2z&=2 \notag\\ 4x+9y-3z&=8\\ -2x-3y+7z&=10 \notag \end{align}\]
怎么做?第一个主元是第一行的2。下面我们想要消去的主元是4,第一个乘数就是4/2=2。我们通过乘以\(l_{21}=2\),然后将其减去来消去第二个方程的主元得到y+z=4。第三行同理,乘数为-1,消去后得到y+5z=12。
然后我们就得到了1y+1z=4和1y+5z=12,接下来就哭呀进一步去消除y了,经过操作后我们原始的\(A\boldsymbol{x}=\boldsymbol{b}\)已经变成了上三角的\(U\boldsymbol{x}=\boldsymbol{c}\)了:
\[\begin{align} 2x+4y-2z&=2 \qquad 2x+4y-2z&=2\notag\\ 4x+9y-3z&=8\qquad \qquad 1y+1z&=4\\ -2x-3y+7z&=10 \qquad \qquad \qquad 4z&=8\notag \end{align}\]
接着回代就可以解了。解出(x,y,z)=(-1,2,2)。行图展示了三个平面通过x的解的点。列图展示了列向量的组合:
\[\begin{equation} A\boldsymbol{x}=(-1)\begin{bmatrix}2\\4\\-2\end{bmatrix}+2\begin{bmatrix}4\\9\\-3\end{bmatrix}+2\begin{bmatrix}-2\\-3\\7\end{bmatrix}=\begin{bmatrix}2\\8\\10\end{bmatrix}=\boldsymbol{b} \end{equation}\]
4×4的或者n×n的方程,消元也是同样的方法:
- 第1列:使用第一个方程在第一个主元下创建0
- 第2列:使用新的方程在第二个主元下创建0
- 第3-n列:持续按上述方法消元来制作上三角U